# Circuitos
# O que são Circuitos?
### Introdução aos Circuitos Elétricos
Um **circuito** é um conjunto de componentes conectados que realizam uma função específica, como acender uma lâmpada ou ligar um motor. Eles são elementos fundamentais e formam toda a base da elétrica!
Para realizar análises de circuitos, é necessário dominar alguns pontos de extrema importância, como:
- **Lei de Ohm**
- **Leis de Kirchhoff**
A partir dessas leis fundamentais, conseguiremos determinar grandezas elétricas como:
- **Tensão**
- **Corrente**
- **Resistência**
Vamos entender melhor ao decorrer deste capítulo!
# Circuitos em Série
No circuito em série, os componentes estão conectados um após o outro, apresentando as seguintes características:
- A corrente elétrica é a mesma em todos os pontos do circuito.
- A tensão elétrica se divide entre os componentes, de acordo com suas resistências.
Utilizando a Lei de Ohm, podemos determinar a tensão em cada componente do circuito.
Resistência Total
A resistência total (Rt) em um circuito em série é obtida somando as resistências individuais:
$R_t = R_1 + R_2 + R_3$
Onde:
- Rt: Resistência total do circuito.
- R1, R2, R3: Resistências individuais dos componentes.
Exemplo
Figura 13: Representação de um circuito em série.
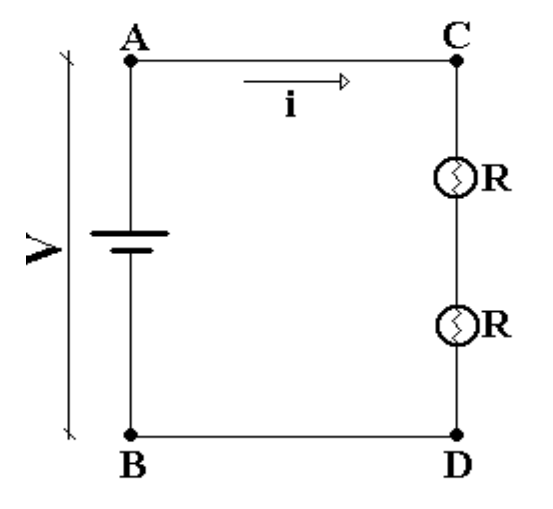
Fonte: UNESP
# Circuitos em Paralelo
No circuito em paralelo, os componentes estão conectados lado a lado, apresentando as seguintes características:
- A tensão elétrica é a mesma em todos os componentes.
- A corrente elétrica se divide entre os ramos do circuito.
Resistência Total
A resistência total (Rt) em um circuito em paralelo é calculada com a seguinte fórmula:
$$\frac{1}{R_t} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3}$$
Onde:
- Rt: Resistência total do circuito.
- R1, R2, R3: Resistências individuais de cada ramo.
Exemplo
Figura 14: Representação de um circuito em paralelo.
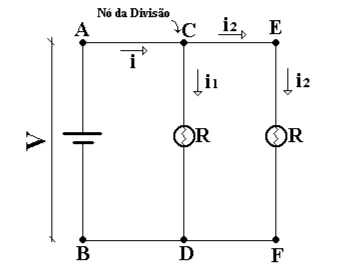
Fonte: UNESP
# Circuito Misto
Um circuito misto é uma combinação de circuitos em série e em paralelo.
Como Calcular a Resistência Equivalente
- Resolva primeiro os componentes conectados em paralelo, utilizando a fórmula:
$$\frac{1}{R_t} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3}$$
- Depois, some a resistência equivalente dos componentes em paralelo com os resistores ligados em série:
$$R_t = R_1 + R_2 + R_3$$
Exemplo
Figura 15: Representação de um circuito misto.
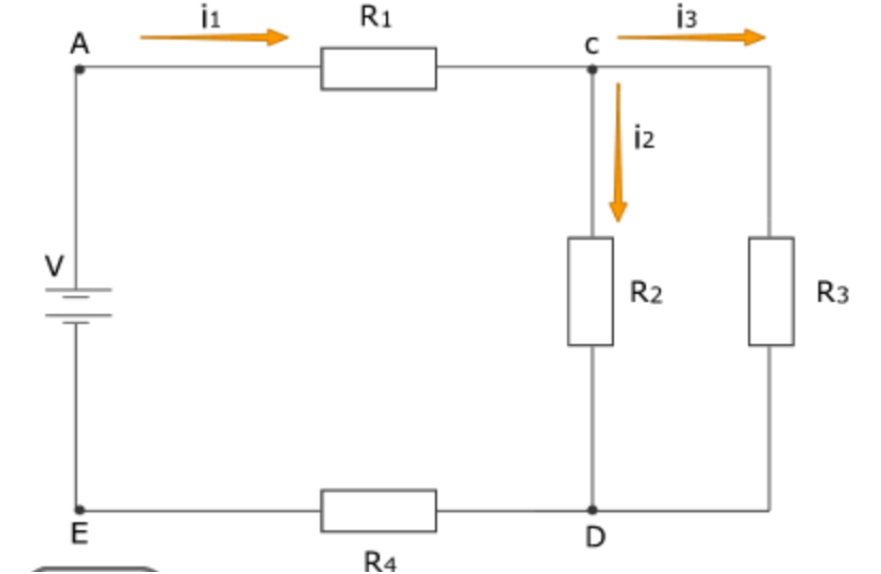
Fonte: IFSUL
# Leis de Kirchhoff
# Lei dos Nós
A **Lei de Kirchhoff das Correntes (ou Nós)** diz que a soma de todas as correntes fluindo para um nó é igual à soma das correntes saindo do nó. Aplica-se para circuitos em série, ou seja, a corrente é a mesma em todos os pontos. Na forma matemática, podemos escrever da seguinte maneira:
$$
\sum i_{\text{in}} = \sum i_{\text{out}}
$$
No nosso cotidiano, um exemplo prático da aplicação da **Lei dos Nós de Kirchhoff** pode ser observado em uma régua de tomadas. Imagine que você conecte dois equipamentos nessa régua: um deles consome **3 A** e o outro consome **2 A**. Nesse caso, a soma das correntes consumidas pelos dois equipamentos será **5 A**. De acordo com a **Lei dos Nós**, a corrente que chega da rede elétrica à régua (**5 A**) será exatamente igual à soma das correntes que saem para alimentar os equipamentos conectados, garantindo o equilíbrio do sistema.
---
# Lei das Malhas
A **Lei de Kirchhoff das Malhas** diz que a soma das tensões em torno de uma malha fechada é **zero**. Isso aplica-se para circuitos em paralelo. Na forma matemática, podemos escrever da seguinte maneira:
$$
\sum V_n = 0
$$
Onde, **n** são todas as tensões presentes em todos os elementos da malha. Para encontrar o valor de cada queda de tensão, você deverá aplicar a **Lei de Ohm** em cada elemento do circuito.
Por exemplo, imagine um circuito com um **resistor** e um **LED** conectados em série. Sabe-se que o circuito é alimentado por uma bateria de **9V**, e para acender o LED é necessário uma tensão de **2V** e corrente de **20mA**. Assim, para que o LED funcione sem ser danificado, é preciso encontrar o resistor ideal.
Subtraindo da bateria a tensão necessária para o funcionamento do LED:
$$
9V - 2V = 7V
$$
A queda de tensão sobre o resistor será de **7V**! Agora, usaremos a **Lei de Ohm** para encontrar o valor do resistor:
$$
V = R \cdot I
$$
Queremos encontrar **R**, então manipulamos a equação:
$ R = \frac{V}{I} $
Substituindo valores:
$$
R = \frac{7V}{20mA} = 350\Omega
$$
Concluímos que, para o funcionamento correto do LED, será necessário um resistor de **350Ω**!
Usando o software de simulação de circuitos **Tinkercad**, montamos esse circuito simples para melhorar a visualização do circuito!
Figura 1: Simulação
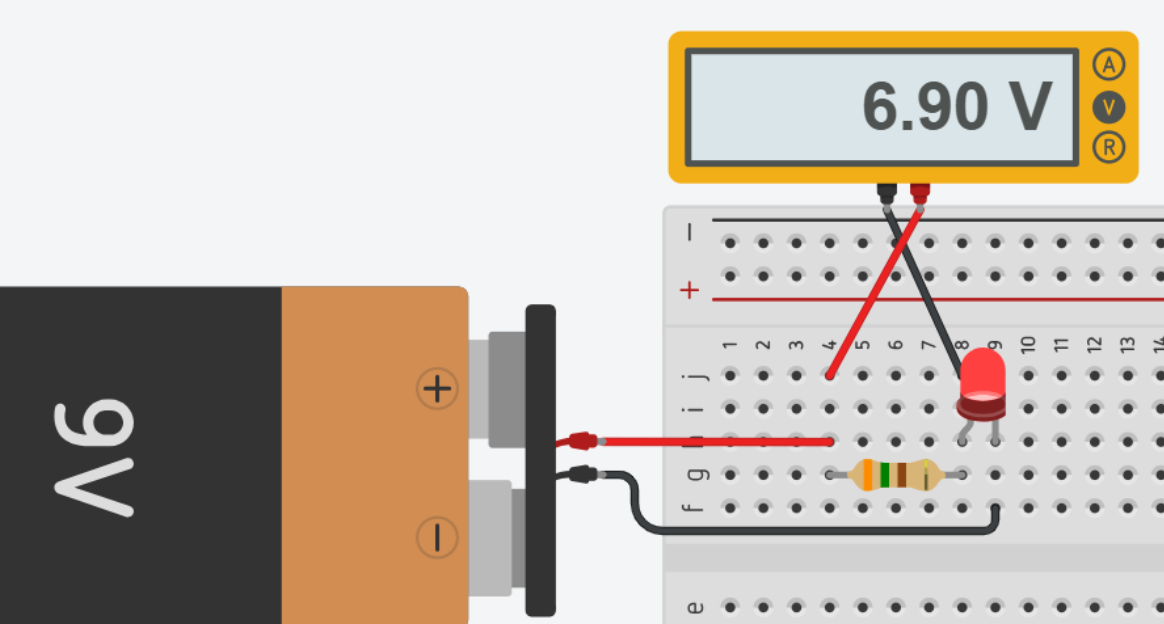
Fonte: Autor
Nos próximos capítulos, iremos abordar com mais detalhes as ferramentas mostradas no exemplo anterior! 